In the world of computers, use the stack or the heap is one important component to ensure the process of handling the data in addition to other things like Queue (queue), linked list, and tree.
Definition 1. Stack is a collection or set of data items organized in the form of a linear sequence, the operating income and the elimination of the data carried on one side [1]
Definition 2. Given a set of ordered sets as S = {S1, S2, ......., ST}, T on the members of S is a linear order, so that the stack of the set have the following information [1]:
1. Top of the stack elements in the set S is said to be TOP, so that:
TOP [S} = ST ............................................ ....................( 1)
2. The number of stack elements in the set S is said to be Noel, so Noel = T, where the set of S can be arranged as:
S = {S1, S2, .........., SNOEL} .............................( 2)
Of the two definitions mentioned above, a stack can be described as follows: 1. An empty stack will have information Noël (S) = 0 and TOP (S) = undefined.
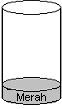
S2. For the stack is not empty, then it will have information as described below where the information is Noel (S) = 1 and TOP (S) = Red
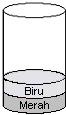
S To stack that contains more than n number of data the information is on the stack contains Noel (S) = 2 (if it contains 2 data) and TOP (S) = Blue as shown in the picture below:
S Elements within the stack mentioned above, has a basic principle in operation is the principle of LIFO (Last In First Out) or entering the rear will have priority to get out the front.
A stack can be described as an array (array) one-dimensional elements ranged from 1 to n elements. Thus, if a stack is defined by n elements then it can be said to be the maximum amount of stack or Noel (S) it is n, so the addition of elements to the stack of n +1 is not allowed or are in the stack overflow condition. It is also valid for the stack with a minimum value of Noel (S) from the stack in state 0, if the retrieval operation performed on the elements of the stack would result in the stack underflow conditions. Two of these conditions is the basis in designing a computer programming application.
2.2. Stack operations In its use of a stack has several operations that can be applied such as making the stack, adding eleme into the stack, menghapusan element of the stack, and other operations associated with the stack.
a) Create (Stack) Create operation (Stack) is used to create a new stack with the name stack, the element value is created when the stack is Noel (S) = 0, TOP (S) = NULL (undefined)
b) isEmpty (Stack) This operation is an operation to check the contents of a stack to be empty or contain. This operation has two (2) boolean conditions are: a. True if the stack is empty or it can be said Noel (S) = 0 b.False if the stack is empty or not in the condition it can be said Noel (S)> 0
c) Push (Stack, Element) This operation is an operation to add one element to the value of X at the top of a stack, so that the position TOP (S) will be worth X, the application of push operations pasa a stack S will result in overflow if Noel (S) of the stack has a maximum value.
d) Pop (Stack) This operation serves to remove one element from the stack S, so that the position Noel (S) will be reduced by one element, and TOP (S) will change. Pop operation can cause underflow condition if a stack S which is in the minimum conditions imposed pop operation.
Postfix infix notationAn arithmetic normally associated with operands and operators. Operand is a character or element whose value is operated with the help of an operator untuik produce a solution.
Suppose if given an arithmetic expression 2 * 3, then the element 'two' and the element of 'three' is the operand of these expressions and elements of '*' is a multiplication operator on two operands that results in a solution. An arithmetic expression can be differentiated into three forms of notation calculations are:
1) prefix notation, if the operator is placed before the two operands 2) infix notation, if the operator is placed between two operands 3) postfix notation, if the operator is placed after the two operands In use, the daily life of notation infix notation arithmetic is the most widely used to express a computation artimatik compared with two other notations, but Postfix notation is a notation used by the compilation engine on the computer with the intent to simplify the encoding process, so that compilation of the stack to the machine requires the expression of the translational process.
Conversion of infix to postfix notation Based on the theory described above, the process of converting infix to Postfix notation in its implementation requires a stack in the process of conversion, while the process has 4 (four) rules are used, namely:
If it finds an opening parenthesis symbol "(" Operation push on the stack will be used to save the symbol into the stack.
If it finds an opening parenthesis symbol ")" Pop operation is used to remove the operators inside the stack.
If there is a symbol of the operator If a strand notation infix operator symbol is found then the operation is performed on the stack consists of:
1.If TOP (S) of the stack is empty or contains the symbol "(" then the push operation will be used to insert the operator into position on the TOP (S)
2.If dipuncak operator stack is an element that has the same level or higher then the pop operation is used to remove the operator followed by a push operation to save the operator scanning the strand.
3.If the operator at the top of the stack has a lower level of the operator who scanned, then the new operator will be directly inserted into the stack with the push operation.
The level of service that is being tracked in order of level are:
Table 1. Operator level in the stack Operator Operator level in the stack
---------------------------------------- ** Supreme * Or / Intermediate + Or - Low
4. If found an operand Operand values are directly used as the output of Postfix notation. Exemplified in an application of an arithmetic expression in infix notation as follows
((A * B) + C / D - E ** F) * G;
The above expression, converted into Postfix notation is described as follows:
Index order to- 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 Characters that will be tracked in infix notation ( ( A * B ) + C / D - E ** F ) * G ; Operators peak (TOP (S) ( ( ( ( ( * ( ( * ( ( ( + ( + ( / + ( / + ( - ( - ( ** - ( ** - ( * * Resultant output in the
form of postfix
A B * C D / + F ** - G *
- Characters that will be tracked in infix notation
- Output produced in Postfix notation Strand
of the above examples, it is converted from infix notation to produce a strand Postfix notation: AB * CD / EF + **- G *
3.2. Stack algorithm implementation
In the PASCAL programming language is defined in the form of a stack algorithm, it is intended to obtain optimal results and targeted when the program was designed and used. From the theory of stack usage in the previous data structures, a stack has two important information that is the TOP (S) which contains information on the content strand in the form of characters and Noel (S) which contains valuable information on the number strand of the stack is an integer.
In its implementation, both the information is packaged in the form of records that contain arrays (array) to restrict the contents of the stack, and provides an index value of the information included in the stack at the time of surgery.
As for the stack algorithm in the form as:
Const
NoelStack = 80;
Type
Eon = Char;
Stack = Record
Top: Array [1 .. NoelStack] of Eon;
Noel: 0 .. NoelStack;
End;
From the algorithm above, the contents of the stack can hold 80 characters that are packaged in the form of records with the name of the stack.
Once the algorithm which contains the basic information of the stack is defined, the establishment of an algorithm for operation of the stack can be arranged in the form of procedures and functions are made himself. The algorithm used for the operation of a stack are:
1) Create Algorithm (S)
This algorithm contains a procedure to create a stack, which gives the condition noel of the stack would be worth zero and the top of the stack are yet to be defined, so that the implementation of the algorithm is to create the stack;
Procedure Create (var S: Stack);
Begin
S. Noel: = 0;
End;
2) Algorithm isEmpty (S)
The algorithm for Boolean operations isEmpty provide information that is true condition (true) or false (False), so that the implementation of these algorithms use a function that is made, which implemented as follows:
Function isEmpty (Var S: Stack): Boolean;
Begin
IsEmpty: = S. Noel = 0
End;
3) Algorithm Push (S, E)
In designing an algorithm for operating the push begins by checking the contents of the stack is full or not. Stack condition would result in a maximum state of the stack overflow error trapping so that the procedure needs to be defined to prevent the overflow condition. The implementation of the push algorithm is:
Procedure Push (var S: Stack; TipeBAru: Eon);
Begin
If S. Noel = NoelStack Then
Stackerror (1)
Else
Begin
S. Noel: Noel S. + = 1;
S. Top [S. Noel]: = newtype
End
End;
4) Algorithm Pop (S)
Last operation of the stack is a pop operation that serves to remove the contents of the stack. As with operations push, pop operations on the use of error trapping used to check the condition stack underflow conditions imposed empty pop operation. The algorithm of this pop is: Procedure Pop (var S: Stack; Var NilaiStack: Eon); Begin If S. Noel = 0 Then StackError (2) Else Begin NilaiStack: = S. Top [s.Noel]; S. Noel: Noel -1 = S. End End; The use of error trapping to push and pop operations are defined further in stackerror algorithm used to determine the condition of a stack overflow or underflow. The error trapping algorithm of this is; Procedure StackError (TingkatanError: Integer); Begin Case level Error of
1: writeln ('Content Stack overflow condition is full ...');
2: writeln ('Fill Empty Stack underflow condition ...') End End;
3: Implementasi Conversion Process notation infix to Postfix Notation From the basic operations that can be applied to a stack, the second phase of the conversion of infix notation to Postfix notation is designing algorithms up the conversion process, by way of comparison the contents of the operator inside the stack to an operator who reads to be included in the stack. The comparison process is viewed based on the level of service set out in the following table:
Table 3. Comparison Operators in the stack and the operator is read Operator Value operator in the stack Value operator which reads ) 0 ( 0 5 +, - 2 1 *, / 4 3 Based on the table an operator that is read and will be incorporated into the stack, first through a process of value comparison with the existing operators in the previous stack. In other words if the meaning of the value of the operator residing in the stack is greater than the value of the operator who reads the operators who are in the stack will be issued until the value is equal or smaller.
Implementation of the algorithm can be described in the form of a function as follows: Function IsiDlmStack (Operator: Char): Integer; Begin Operator Case Of '(': IsiDlmStack: = 0; '+','-': IsiDlmStack: = 2; '*','/': IsiDlmStack: = 4; End End; Isidlmstack function mentioned above is the function of the level of service that its position is in a stack, as for function to determine the level of service that is read is: Function Stackyangdibaca (Operator: Char): Integer; Begin Operator Case Of ')': Stackyangbaca: = 0; '+','-': Stackyangbaca: = 1; '*','/': Stackyangbaca: = 3; '(': Stackyangbaca: = 5 End End; After checking the functions performed, a process that needs to be designed next is establish a procedure to save the operator that is read into an array of implementation arrangement was made as follows: SimpanChar Procedure (Ch: Char; Var Ekspost: TipeEks; Var Indekspost: TipeIndex); Begin Indekspost: = Indekspost + 1; Ekspost: = ch End; With this procedure the operator of storage into an array of the above, then the process of converting infix notation to Postfix notation language arranged in the
form of the algorithm as follows [2]: Procedures KonversiInfixKePostfix
1. Read the length of a strand of characters
2. Create Stack
3. Operator Push '(' to Top of Stack
4. n: = 0 5. For K: = 1 To length of a strand + 1 do If k is a strand to the operand then Remove the strands into K in the form of Output Else While the operator value dal; am stack> operator is read do Fill pop operators from the stack Remove the operator is in the form of output End While If operator to K = ')' then Pop operators from the stack contents Else Operators Push into the stack End If End If Strand length; = n 6. End For With a view on the above conversion algorithm, design the algorithm in the Pascal programming baha structured as follows: InfixkePostfix conversion procedure (ex within: Type ex; pjg within: This type of index; var ekspost: Type Ex; var long post: Type index); Var opstack: stack; indeksdlm, post index: type index; chdlm, operators, store: char; Begin create (Opstack); Push (Opstack,'('); eksdlm [pjg within +1]: = ')'; Post index: = 0; For indeksdlm: = 1 to pjgdlm +1 Do Begin chdlm: = Ex-DLM [index within]; within if ch in ['A'....' Z'] then store char (ch DLM, Ekspost, indekspost) Else Begin While isidlmstack (top of stack (opstack))> stack is read (ch within) Do begin pop (opstack, operator); simpanchar (operator, ekspost, indekspost) end; if chdlm = ')' then pop (opstack, save) else push (opstack, save) end long post: = indekspost end; long post: = indekspost end; Dish full of the conversion process notation infix to Postfix notation in the Pascal language that is ready to be applied are described under the heading of this 4. CONCLUSION Application conversion infix notation to Postfix notation is one means to be able to know the process of compiling arithmetic in the machine. Use of stack can also be used for other methods such as making matching parentheses, or in addition to its use in the palindrome test the conversion process of this notation, the need to understand is a stack is essentially an array that contains two important information that is Noel that serves to know the number of stacks and TOP which serves to determine the peak position of a stack. Stack also has two conditions that can cause errors is if stack underflow condition is surgery performed on an empty data capture (pop) and the condition of overflow if the stack is fully carried out the operation of adding the data. Both of these positions can cause the stack in an invalid so that the use of error trapping to accommodate conditions need to be considered invalid. Infix notation commonly used by various groups in performing an arithmetic calculation process can be *** compiled into Postfix notation used by the machine so that the compilation of knowledge about the use of arithmetic notation will be broader. REFERENCES [1] Loomis, Mary ES, Data Management and File Processing, Prentice-Hall, Inc.., Englewood Cliffs, New Jersey, 1985. [2] Horowitz, E and S. Sahni, Fundamentals of Computer Algorithms, Computer Science Press, Potomac, Maryland, 1978. [3] McCracken, Daniel D., A Second Course in Computer Science with Pascal, John Willey & Sons, City College, New Listing Program {Programme Name: Konversi.Pas Authors: Okay Hendradhy Version: 1.0 } Uses crt; const Noelstack = 80; Makschar = 80; Type Eon = char; stack = Record Top: array [1 ... Noelstack] of Eon; Noel: 0 ... Noelstack; End; Tipeindex = 0 ... makschar; Typeeks = array [1 ... Noelstack] of char Var again: char; {Forms of stack operations} Function isEmpty (var s: stack): Boolean; Begin IsEmpty: = s. noel = 0 End; Procedure create (var stack s); Begin S. Noel: = 0; End; buatkosong procedure (Var stack s); Begin S. Noel: = 0; End; Procedure stack error (level Error: integer); Begin Case error rate of
1: Writeln (the contents of the stack already too full);
2: Writeln (fill an empty stack); End End; Procedure push (var s: stack; new type: Eon); Begin If s. Noel Noel = stack then Error stack (1) Else Begin s.Noel: = s. Noel +1; s.Top [s.Noel]: = new type End End; Procedure pop (var s: stack; var stack value: Eon); Begin If s. Noel = 0 then Stack error (2) Else Begin stack value: = s.top [s.Noel]; S. Noel: = s. Noel - 1; End End; {The process of converting an expression} Function stack top (s: stack): Eon; Begin Peak stack: = s.top [s.noel] End; content in stack Function (operator: char): integer; Begin case operator of '(': content in stack: = 0; '+','-': content in stack: = 2; '*',','/': content in stack: = 4; End End; read Stack Function (operator: char): integer Begin Case operator of ')': read Stack: = 0; '+','-': read Stack : = 1; '*','/': read Stack: = 3; '(': read Stack: = 5; End End; Procedure simpanchar (ch: char; Var ekspost: Tipeks; Var index post; Type index); Begin indec post: post = index +1; ekspost [index post]: = ch; End; Infix to Postfix conversion procedure (ex within: Type ex; pjg within: This type of index; var ekspost: Type Ex; var long post: Type index); Var opstack: stack; index in, post index: type index; chdlm, operators, store: char; Begin create (Opstack); Push (Opstack,'('); eksdlm [pjg within +1]: = ')'; Post index: = 0; For indeksdlm: = 1 to long in +1 Do Begin chdlm: = Ex-DLM [index within]; within if ch in ['A'....' Z'] then store char (ch DLM, Ekspost, indekspost) Else Begin While content in stack (top of stack (opstack))> stack is read (ch within) Do begin pop (opstack, operator); save char (operator, ekspost, indekspost) end; if chdlm = ')' then pop (opstack, save) else push (opstack, save) end long post: = indekspost end; long post: = index post end; Produce conversion of expression; var long in index, long post: type index; eksdlm, ekspot: type ex- begin again: = 'y'; While (upcase (again) = 'x' do Begin clsscr; long in: = 0 do while not eoln begin long in: = long in +1; read (eksdlm [long in]) end; readln; write ('infix expression:'); for index: = 1 to long in do write (eksdlm [index]); writeln; konversiinfixkePostfix (eksdlm, panjangdlm, ekspost, long post); write ('in the form of Postfix') for index: = 1 to long post do write (ekspost [index]); writeln; writeln; write ('no data again <y/t>.'); readln (again) end; End; begin conversion of expression; end In computer science, stack or heap is a collection of objects that use the principle of LIFO (Last In First Out), ie data terakhr entered will be the first out of the stack. Stack can be implemented as a linked representation or kontigu (with table fix). Stack Characteristics: TOP element (the peak) is known penisipan and removal of elements is always done at TOP LIFO Stack Utilization: Calculation of arithmetic expressions (Postfix) backtraking algorithm (trace back) recursive algorithm Stack operations are usually: 1.Push (input E: typeelmt, input / output data: stack): adds an element onto the stack 2.Pop (input / output data: stack, the output E: typeelmt): remove an element stack 3.IsEmpty () 4.IsFull () 5.dan beberapas other selector


 Bact to Top
Bact to Top





 11:45:00 PM
11:45:00 PM
 Dwi
Dwi